From Circle to Hyperspheres
Episode II :
Odd Isometries,
Generalized Tonnetze, Spectral Applications.
Chapters
- 10 Odd Isometries
- 11 Hypersphere of Tonnetze
- 12 Morphing in 2D
- 13 Morphing in 4D
- 14 Hypersphere of Spectra
- 15 Hypersphere of Spectra : Views
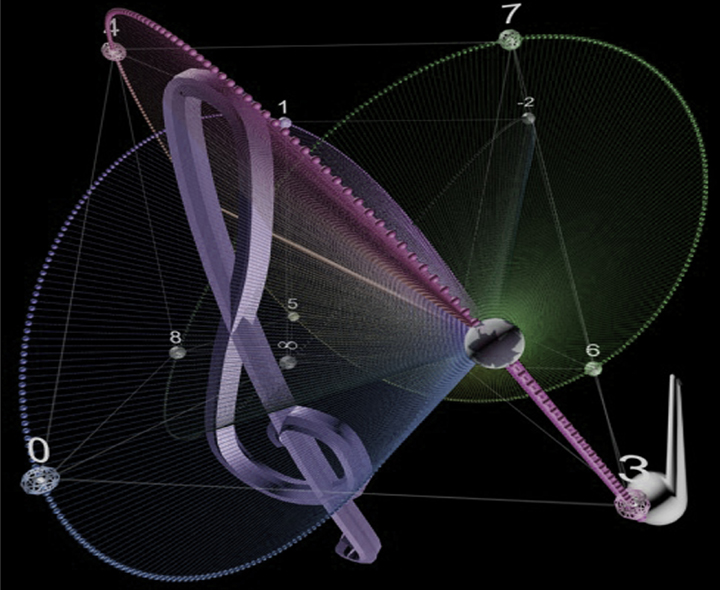
->Some isometries in the Tonnetz discovered by G. Mazzola and formalized in the 4D space by Emmanuel.Amiot and Guillaume Baxias.
->Hypersphere of Tonnetze, is a graphical illustration of the work initiated by Louis Bigo to project and represent the generalized Tonnetze T1 to T6 on the surface of the 4D Hypersphere.
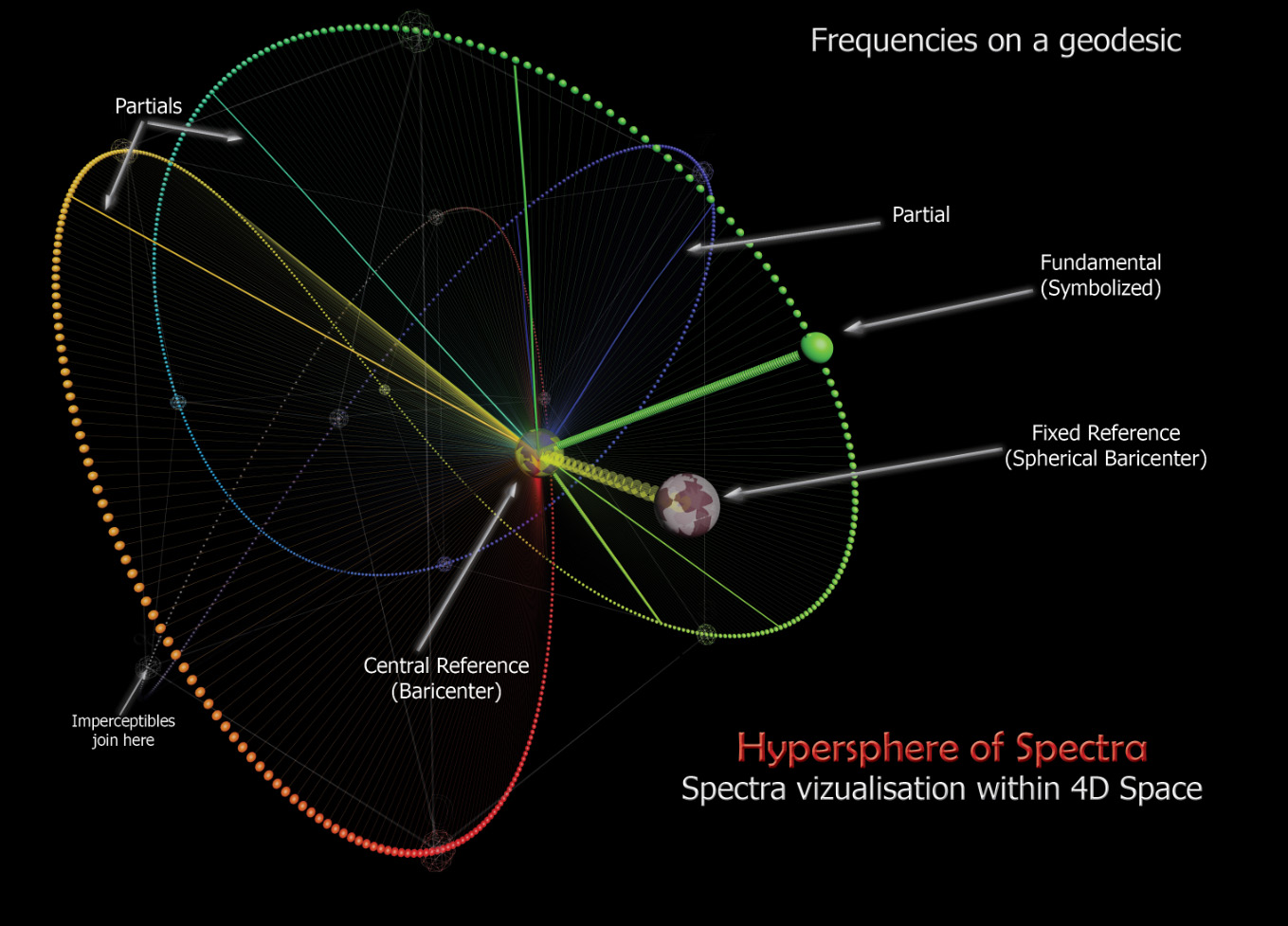
->The Hypersphere of Spectra (developed w. Stéphane de Gérando), is an original way to display any sound according to its spectra, within a 4D environment.
Premiered at Mc Gill University Montréal, 2013
Embeded Youtube Playlist :
From Circle to Hyperspheres Chap 10 Odd Isometries
The Planet Model features 48 isometries,
The 4th dimension enables to represent visually the unusal ones.
Work together with Emmanuel Amiot
The chords feature the same form on the Hypersphere but their ...function is different:[+] Show More
The 4th dimension enables to represent visually the unusal ones.
Work together with Emmanuel Amiot
The chords feature the same form on the Hypersphere but their ...function is different:[+] Show More

From Circle to Hyperspheres Chap 10 Odd Isometries
The Planet Model features 48 isometries, The 4th dimension enables to ...

From Circle to Hyperspheres Chap 11 Hypersphere of Tonnetze
Lines in 2D becomes Geodesics in 4D. The Hypersphere of Tonnetze, is a ...

From Circle to Hyperspheres Chap 12 Morphing in 2D
A music path can be drawn on a 2D Graph : a Tonnetz. If we modify this ...

From Circle to Hyperspheres Chap 13 Morphing in 4D
As above in 2D, a music path can be drawn on a 4D Hypersphere. The ...

From Circle to Hyperspheres Chap 14 HyperSphere of Spectra
For application to spectral music, we propose a correspondence ...

From Circle to Hyperspheres Chap 15 HoS Views
Since the user centric vizualisation used in all Planet-4D may appear ...

Chap 16 End Credits
End Credits,
Please refer to my Papers Section for scientific description,